المثلثات
المثلث هو
أحد الأشكال الأساسية في الهندسة، وهو
شكل ثنائي الأبعاد مكون من ثلاثة رؤوس تصل
بينها ثلاثة اضلاع، وتلك الأضلاع هي قطع
مستقيمة يمكن تصنيف المثلثات إلى نوعين :
أنواع
المثلثات حسب
الاضلاع و
أنواع المثلثات حسب الزوايا
من الممكن تصنيف المثلثات تبعا لأطوال أضلاعها كما يلي:
مثلث متساوي الاضلاع:
هو
مثلث جميع أضلاعه متساوية، وتكون جميع زوايا المثلث
متساوي الأضلاع متساوية أيضا، وقيمة كل منها 60 درجة.
مثلث متساوي الضلعين:
ويسمى
أيضا متساوي الساقين، هو مثلث فيه ضلعان متساويان. الزاويتان المقابلتان
لهذين الضلعين تكونان متساويتين أيضا.
مثلث مختلف الأضلاع:
هو مثلث أطوال أضلاعه مختلفة، زوايا هذا
المثلث تكون مختلفة القيم أيضا.
اما
التصنيف الاخر
فهو تبعا لقياس الزوايا الداخلية في المثلث:
مثلث قائم الزاوية: له زاوية قياسها 90 درجة (زاوية
قائمة)، يدعى الضلع المقابل للزاوية
القائمة بالوتر، وهو
أطول أضلاع هذا المثلث.
مثلث منفرج الزاوية: له زاوية قياسها أكبر من 90 درجة وأصغر
من 180 درجة(زاوية منفرجة)
نظريات
حول العلاقة بين اضلاع
المثلث وزواياه
1)
الزاوية الخارجية في المثلث اكبر من اية
زاوية داخلية ما عدا المجاورة لها
2)
الضلع الاكبر
في المثلث تقابله الزاوية الكبرى
3) مجموع أي ضلعين في أي مثلث اكبر من
الضلع الثالث
مستقيمات خاصة بالمثلت
1) منصف
زاوية:
هو مستقيم يخرج من رأس زاوية المثلث
ويقسمها الى
قسمين متساويين, في المثلث يوجد ثلاثة منصفات زوايا.
2) متوسط:
هو مستقيم يصل رأس المثلث مع منتصف الضلع
الذي يقابل هذا الرأس ,في المثلث ثلاثة مستقيمات متوسطة.
3) عمود منصف:
هو مستقيم يخرج من منتصفات ضلع المثلث
ويكون عموديا على الضلع ,وفي المثلث ثلاثة اعمدة
منصفة.
تطابق مثلثات:
تعريف: المثلثان اللذان اضلاعهما وزواياهما الثلاثة متساوية بالتناسب يسميان مثلثان متطابقان.
نظريات التطابق:
1)ينطبق المثلثان كل على الاخر اذا تساوا بضلعين والزاوية المحصورة بينهما.
2) ينطبق المثلثان كل على الاخر اذا تساوا بزاويتين والضلع المحصور بينهما.
3) ينطبق المثلثان كل على الاخر اذا تساوا بثلاثة اضلاع
تشابه مثلثات:
تعريف: يُقال عن
شكلين أنهما متشابهان إذا كان أحدهما مطابقا للآخر بعد إجراء
تحجيم عليه (تكبير أو تصغير)
1)
يتشابه مثلثان
إذا تساوت زاويتان من المثلث الأول مع زاويتين في المثلث الثاني.
2)
يتشابه مثلثان
إذا تناسبت أطوال الأضلاع المتناظرة فيهما.
3)يتشابه
مثلثان
إذا تساوى قياس زاوية من مثلث قياس زاوية من مثلث آخر و
تناسبت أطوال الأضلاع التي تحتويهما هاتين الزاويتين فإن المثلثين يتشابهان.
نظرية فيتاغورس:
تستعمل هذه النظرية لحساب طول الضلع الثالث
اذا
اعطي
طول الضلعين الاخرين.
هذه النظرية تستعمل فقط بمثلث قائم
الزاوية.
القانون







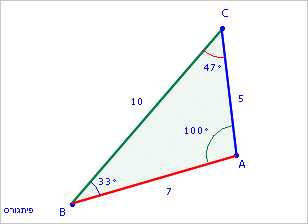









.jpg)


.jpg)
אין תגובות:
הוסף רשומת תגובה